Klaassen & Magnus's 22 Myths of Tennis - Myth 9
After Alexander Zverev took the first set in 6-4 against Dominic Thiem at Saturday’s BMW Open semifinal, it looked like he was on track to stop the Austrian’s 29th ATP singles win this season. But the tables quickly turned and after taking the second sets in 6-2 and 6-3, Thiem ultimately prevailed, securing a spot in the final against Philipp Kohlschreiber.
When these kind of game reversals occur in a match, it is tempting to look for explanations. The player who has lost his lead all of a sudden seems less determined than before, more error prone, or just out of steam. It’s harder to accept that the reversal could simply be due to chance; that winning the first set and losing the second doesn’t indicate that a player’s ability has changed but that he simply was luckier in the first.
It’s interesting that, while we tend to ignore the role of random chance in this context, we seem to accept it in other settings. We would probably all agree, for example, that awarding a match to the player who was the first to win 10 points would be a bad idea. Why? Because, over such a small number of points, even a mediocre player could hit a streak and win out. More points are needed to let each player’s true underlying ability to overcome randomness.
Myth 9: “Summary statistics give a precise impression of a player’s performance”
This brings us to Klaassen and Magnus’s 9th Myth of Analyzing Wimbledon. This one concerns standard match summaries and how informative they are about player ability. K&M focus specifically on game scores within sets and what they indicate about a player’s performance.
Clearly, a player who has won fewer games in a set is also likely to have won a smaller percentage of points on serve than his opponent. Going back to the Zverev-Thiem match, for example, Zverev won 59% of points on serve in the first set of the Munich semifinal compared to Thiem’s 53% but only 52% in the second set compared to Thiem’s 65%. So it shouldn’t be a surprise that Zverev one the first set but ceded the second to Thiem.
But the question isn’t about what game spreads tell us about the observed performance. It is what they tell us about a player’s ability, which is something we can never truly observe.
Mathematical models of tennis effectively treat each server as though he has an internal dial that is set to his chance of winning a point on serve against a specific opponent. So when K&M think about “player performance”, it is the setting of that internal dial that they are interested in. Was it 59% for Zverev’s serving against Thiem? 53%? or something else?
The thing that is sometimes hard to wrap our heads around is that, even if a player has a fixed dial set to X%, many combinations of points won, games won, etc. are still possible. One way to see this is to consider the typical game spread in a set when each player’s true percentage of points won on serve is fixed. The heatmap below shows the range in game spread for a variety of combinations of serve percentage. Here, the range is the difference in the 10% largest game spreads in 10,000 simulated sets minus the 10% smallest game spreads. If 3 simulated sets had scores 6-2, 1-6, and 3-6 the game spreads would be +4, -5, and -3, which would have the largest spread of 5 and the smallest of 3.
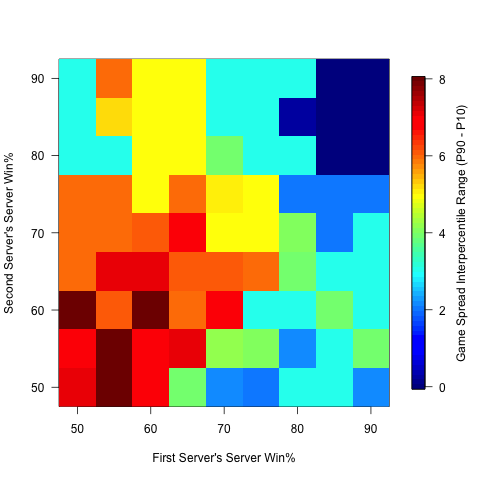
The above plot shows that in the 50-70% range, chance alone would result in a lot of variety in game scores as the 90% range in this region has a game difference of 4+. Zverev and Thiem were in the 50-60% range that had an even higher range of 6+, which tells us that a reversal in game spreads from one set to the next wouldn’t be all that unusual. And, more importantly, wouldn’t necessarily mean that any player was playing unusually above or below his ability.
All of this isn’t to say that some players aren’t up-and-down. We can look to the other Munich semifinal and find a prime candidate for a truly mercurial player in Fabio Fognini. But, in general, these types of players are the exceptions and we tend to underestimate how many up-and-down performances are due to plain ol' random luck.

