Are Top ATP Players Non-IID?
With sport at a standstill, there is ample time for sports nerds to get really wonky. In this post, I look at a question that should go to the heart of any tennis analyst: are players non-iid? I look at how we can measure non-iid effects, why we should care, and who has been the most non-iid among the Top 50 ATP players.
In one of the rare sports papers to appear in JASA, the two giants of tennis statistics, Klaassen and Magnus, evaluated the iid assumption for point outcomes in tennis. If you have ever done a regression analysis, you already have experience applying the “independent and identically distributed” assumption. For a random sample of observations, iid is a reasonable and convenient starting point. In the context of tennis, iid is the simplest way of thinking about the sequence of point outcomes in a match. Essentially, once we know a player’s average serve point won for the match we assume that every point on their serve is a Bernoulli trial with the chance of success equal to their match serve win probability.
From a statistical point of view, iid is a real boon for analysis. If players are iid, then any event of interest, whether winning a set, or winning a tiebreak, or winning a match, boils down to some function of each player’s serve win probability.
But what if they aren’t iid? Well, then things get more complicated. Non-iid would mean players serve systematically better or worse in some situations, like say, all 30-30 points for example. We would need to know those tendencies to have any hope of describing the probabilities of outcomes within a match.
If you have ever found yourself saying a player has gotten tight or choked during a match, then you were talking about non-iid effects. We are all so use to seeing narratives in the progress of a tennis match that it is hard to accept that players could actually be iid. That apparent streaks or surprises we see are all consistent with the chance involved with a Bernoulli sequence.
If the study of Klaassen and Magnus teaches us anything, it is that the truth is somewhere in-between. What I mean is that, players are not iid but their non-iid effects are much smaller than our intuition would suggest. So small, in fact, that the iid assumption is a really close description of actual results in tennis for many cases.
Although the effects may be small on average, it is still possible that individual players show greater non-iid behavior than others. This got me to thinking about who among the current top men’s players would be least iid?
One way to get an overall measure of non-iid effects in a match is to compare a player’s actual service games won against the iid-predicted service games won. Let’s call $g$ the actual proportion of service games won in a match. Now, take the player of interest’s proportion of points won on serve in the match as $p$ and their opponent’s serve win proportion as $q$. We can use a Monte Carlo to get an expected proportion of games won $\hat{g}(p, q)$ given the match serve characteristics.
To give a specific example, in his last match before the current suspension of tour play, Novak Djokovic won 90% of service games, with a win percent on serve of 70% against Stefanos Tsitsipas' 58%. So we would plug the 70% and 58% serve chances into the iid simulator for a best of 3 match and get the estimated service games won for some large number of simulated matches.
I carried out this simulation for matches between 2018 and the present for all Top 50 ATP players (whatever those rankings still mean!). The chart to the right shows the results for all matches with the average non-iid in blue. The players are sorted from most positive average non-iid to least from top to bottom. Here, a positive effect means a player won more service games than expected given their serve win percentage on points and an iid assumption.
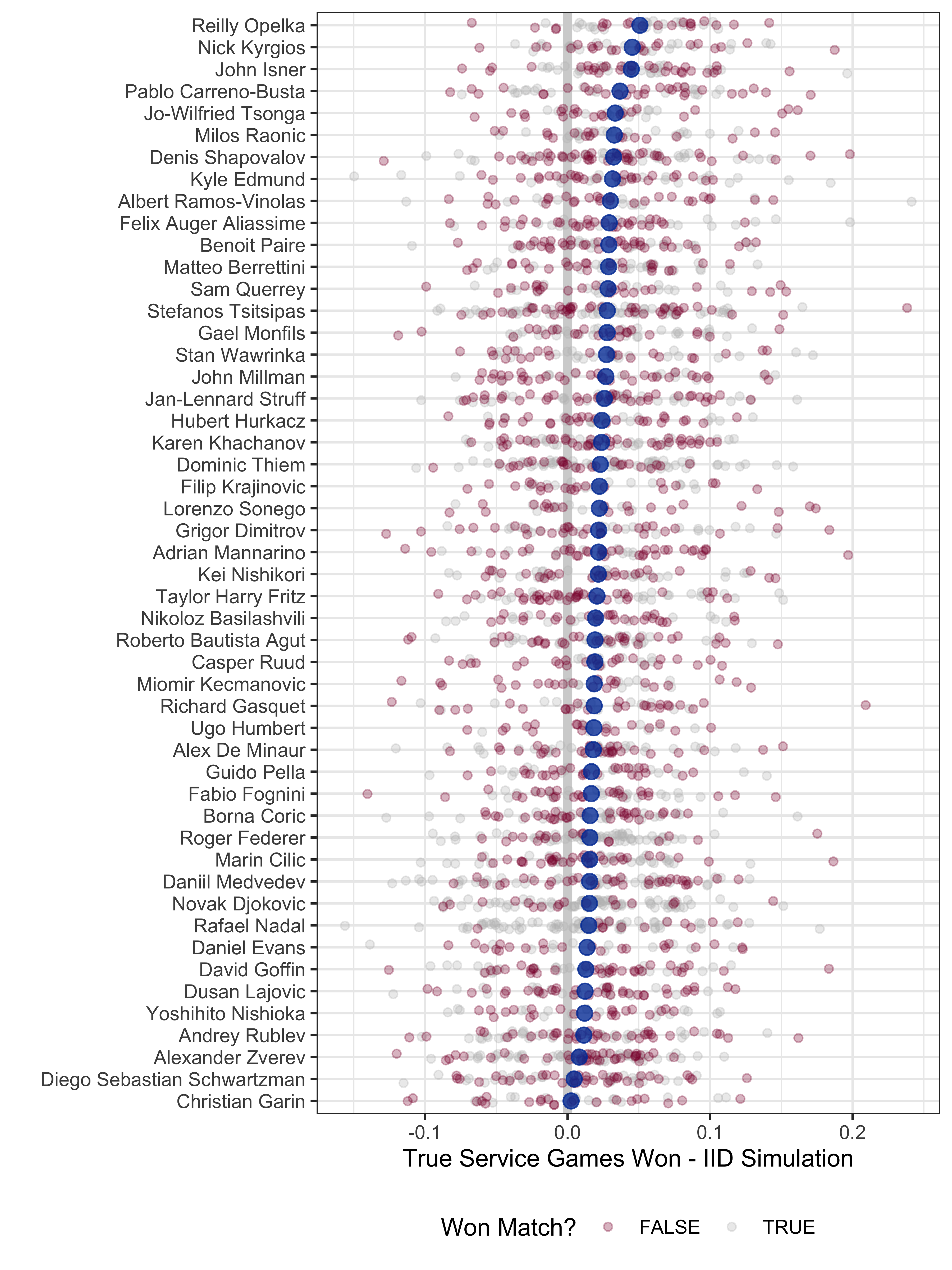
Right at the top are three of the biggest servers among the players: Opelka, Kyrgios, and Isner. What could explain this? One possibility is that, for players for whom the serve is a real weapon, they may have one or two very effective serve strategies that they will go to on the most important points, say in close service games or in end-of-game situations. This would be one way in which a player could up their overall performance on service games won, while their average percentage of points won on serve may be largely unchanged.
It is interesting to find several players we don’t think of as especially strong servers in the top 10. Players like Carreno-Busta, Tsonga and Shapovalov. The non-iid effect is less for these players but it may still be driven by the same strategy. Although these players may have an overall lower percentage of points won on serve, they may still have some set strategy or even mindset on the most important points of serve that result in this measurable gap between the iid prediction and non-iid prediction.
Taking the case of Carreno-Busta, his top 3 matches in terms of the iid effect were each loses, where his opponents were serving at an over 70% win percentage. Carreno-Busta won 90% or more of service games won in each case despite a comparatively low percentage of points won on serve. There was the 2019 loss to Denis Shapovalov in Rome, where Carreno Busta won +17 percentage points of service games compared to the iid expectation; the 2019 loss in Shanghai to Dominic Thiem where he won +14 percentage points more than expected; and the recent loss in Rotterdam to Felix Auger Aliassime where he won +13 percentage points. This group of cases makes the point that non-iid effects could highlight cases where a player was handling pressure well on serve, but still managed to lose.
I wasn’t too surprised to find the Big 3 among the players that are most consistent with iid. It means that they been among some of the least sensitive too context. Or, put another way, these are the players who play every point like it is equally important. Something that many attribute to the mentality of a champion player.
Sharp-eyed readers may note that more players are on the positive side of the non-iid effect than the negative side. I think this may be partly due to the fact that, owing to the small number of service games played in a match, especially best of 3, the outcome is more like a discrete outcome with an upper bound of 1.
We could use a similar setup to look at other measures of performance, aside from service games won, that may be more sensitive to non-iid effects. There seems no end of interesting things to investigate with non-iid and this may be something I’ll delve into further in some future posts.