Slam Seeding - Is 16 Better than 32?
Starting in 2019, Grand Slams will have just 16 seeds. Top players have expressed concerns that this change will make it harder for them to advance to the latter stages of Majors and make for less competitive matches as the events progress. Are they right?
As the 2018 Australian Open was winding down, Tumaini Carayol published a piece for The Ringer on ‘The Battle Over the Future of Tennis’. The focus of the article was a series of changes the Grand Slams were set to roll out over the coming years with, in their view, little or no input from players, spurring calls among players for unionization.

In his discussions over the changes with players, Carayol, who was often the first to make top players aware of the plans underway, discovered that the change to Grand Slam seeds was one of the most worrisome to them.
The change that is planned is to drop seeds at Grand Slams from 32 to 16, a change the Grand Slam Board has already decided will go into effect in 2019.
The 2019 change will mark a return to the way seeding use to be done, a time that some stalwarts of the game, like Roger Federer, can still remember. Federer has actually embraced the return to former times but most players have been critical of the move. The whole point of introducing 32 seeds way back when was to provide more protection for the top 30 players, at least through the first two rounds, as they would be assured not to have to player another top 30 player before the 3rd round. Without that protection, players are concerned that it will become that much harder for the best players to advance to the second week.
While there are multiple reasons why players are feeling frustrated with this planned change, one of the main ones is that the consequences of the change are so unclear. If an impact study was done, it was not made available to the public or to the players, leaving us all to guess at whether 16-seed Majors will be better or worse for the sport.
Since we do have ways to simulate the outcomes of tournaments with reasonable accuracy, we can use this method to test how reverting back to 16 seeds could change outcomes at Grand Slams.
Match Competitiveness
Here is how the simulation works. I start with all of the draws for the 2017 Grand Slams. The 32 seeds are fixed as they were in the official draw. The actual progress of the “32 seed” event is based on player Elo ratings at the start of the event. For one simulation, the result for each match in a given round is a random draw from a Bernoulli distribution (a toss of a coin) where the chance the stronger player wins is based on their Elo prediction. This is carried through to each round until a winner is decided.
The only difference in the “16 seed” simulation is that we randomly shuffle the positions of all players but the top 16. This is done at the start of each simulation.
For each of the 4 slams, 5,000 simulations are run for both the 32-seed and 16-seed condition. The actual summary of the outcomes for each seeding condition combine across all 4 events to protect against any peculiarities in the choice of seeds that might have been present in one event or another.
So what exactly are the outcomes we consider?
From the discussion over the seeding change, it seems the two main worries are around the 1) competitiveness of matches and 2) early upsets. To get at the first, we can look at the frequency of close matches in each round when a Major uses 32 versus 16 seeds. If 16 seeds create tighter matches earlier, we would expect to see a greater frequency of close matches in initial rounds.
If we consider a “close” match to be one in which the expected winner and loser are separated by a win margin of 30% or less, the simulation of men’s Grand Slam matches show clear differences in match competitiveness between 32 and 16-seed events in the first 5 rounds.
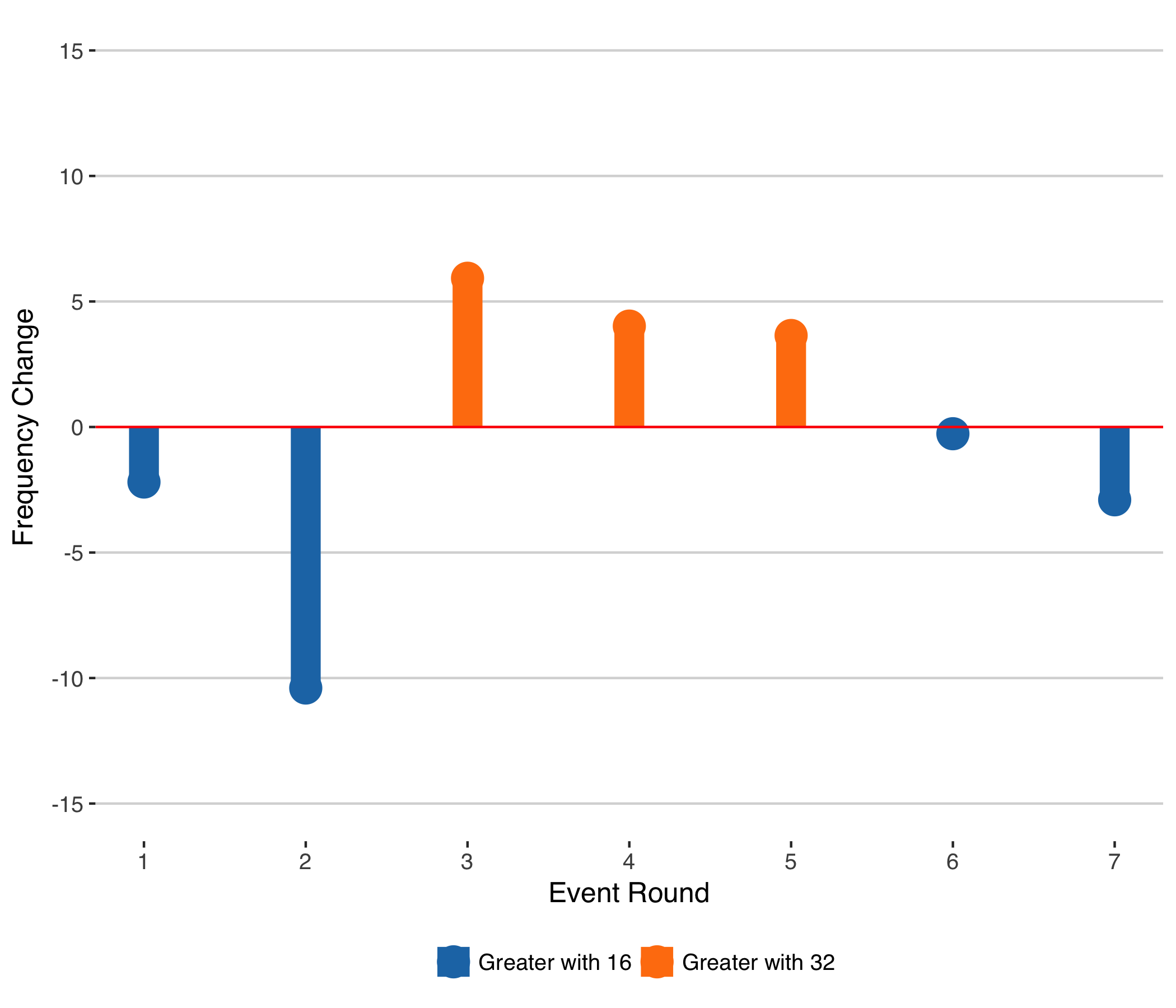
Change in Frequency of Close Matches by Round with 16-seed Men's Grand Slam
In the first two round, 16 seed events result in a higher frequency of close matches, increasing close first round matches by 3 percentage points and close second round by 10 percentage points. The flip side of those early close matches is to see fewer tight matches in rounds 3 to 5, the 3rd round getting the biggest hit.
When we look at the impact for the women’s draw, we find a similar pattern but with the early-round effect of the 16 seed draw lasting one additional round. In other words, we would expect more competitive matches in round 1 to 3 with 16 seeds and less competitive matches in all subsequent rounds.
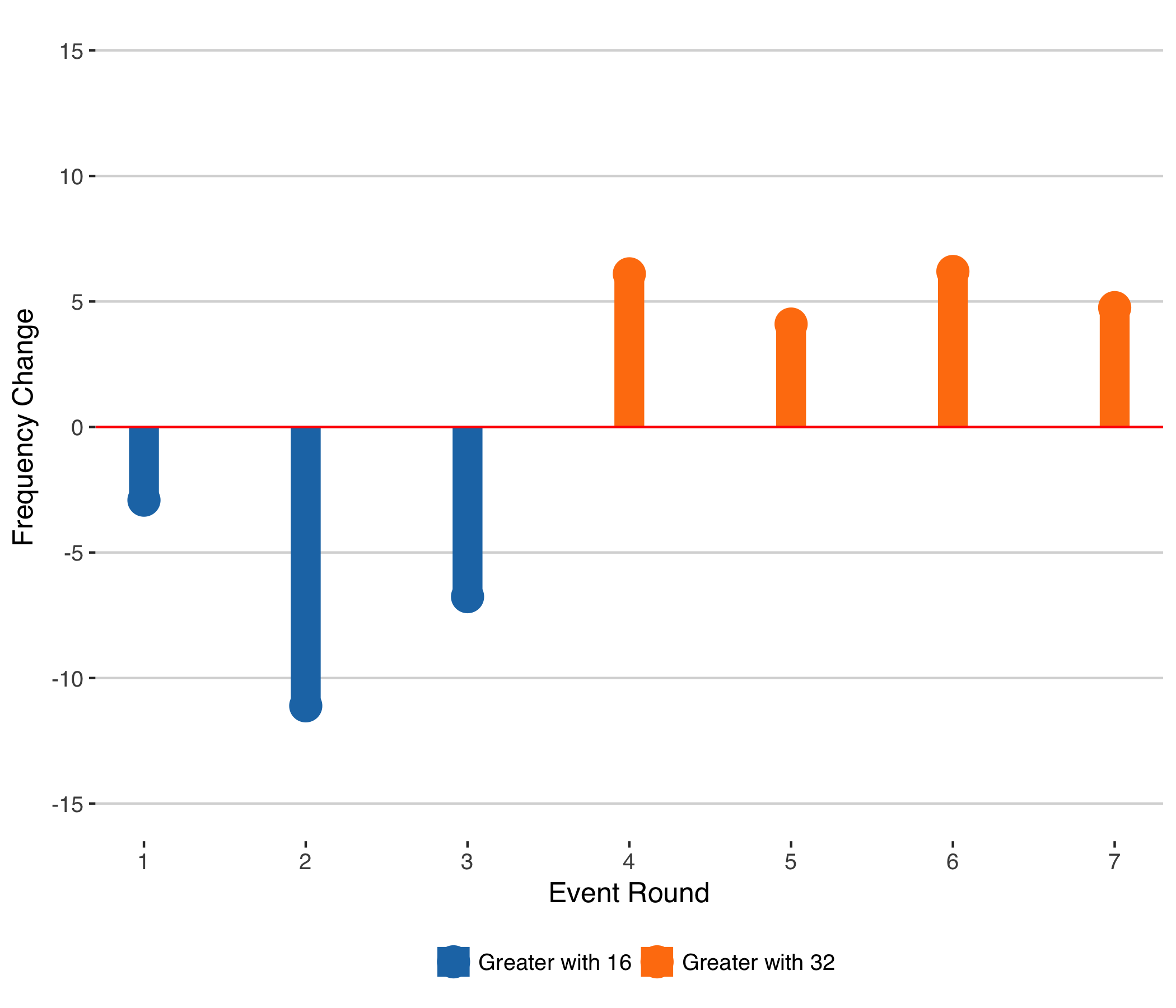
Change in Frequency of Close Matches by Round with 16-seed Women's Grand Slam
Interestingly, while the frequency of close matches in the semifinals and finals of the men’s tournament would appear to be unaffected by the number of seeds, we can expect a 5 percentage point reduction in close semifinals and finals for a 16-seed women’s Major.
Just Results
There are probably no end of opinions about what makes a Grand Slam ‘great’. But I think most of us agree that a good property for a tournament to have is that players earn the results that are most consistent with their performance ability. I am calling this property ‘just results’.
To look at the appropriateness of the results across rounds, we can derive a player’s expected round from their Elo ranking going into the event. If a player is the highest ranked player, their expected round is 7, while if a player is the 128th ranked their expected round is 1. When the actual round reached is not equal to the expected round, it suggests that the design of the tournament may be flawed.
Let’s first have a look at how the actual and expected round reach is expected to vary with 32 and 16-seed men’s Grand Slams for the first 3 rounds. We can see some big effects in the first and third round. With a 16-seed draw, there is a large number of players who should end their slam in the first round who would advance to the second and third rounds. On the other hand, more players who should be getting to the 3rd round would get upset in the first.
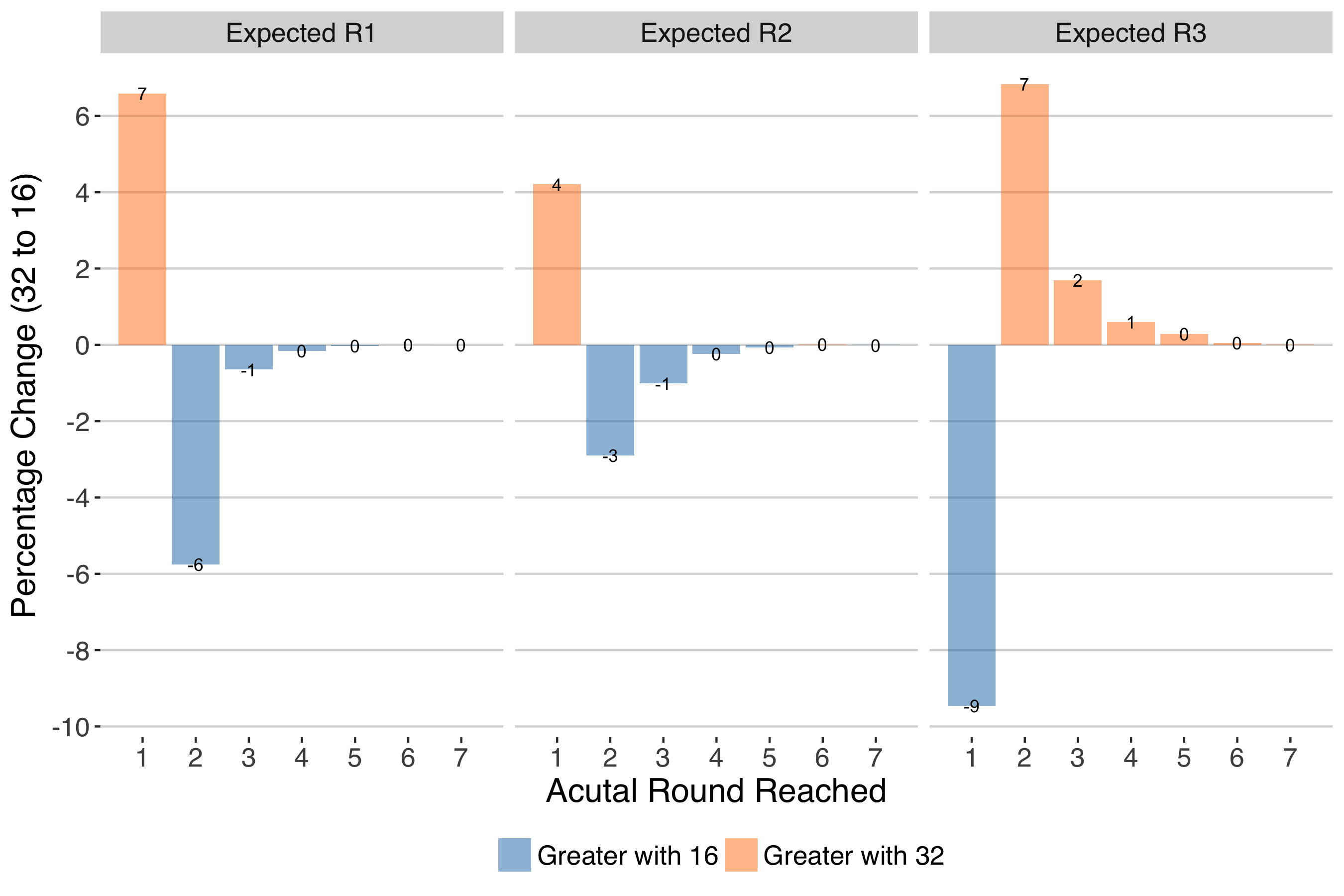
Actual and Expected Round Changes for R1-R3 with Men's 16-seed Grand Slam
Effects in the 4th and 5th round also so some strong differences, primarily in the first and second round. We see that the 32 seed would be more likely to advance the better players. After the 5th round, the pattern is similar but the differences are much smaller.
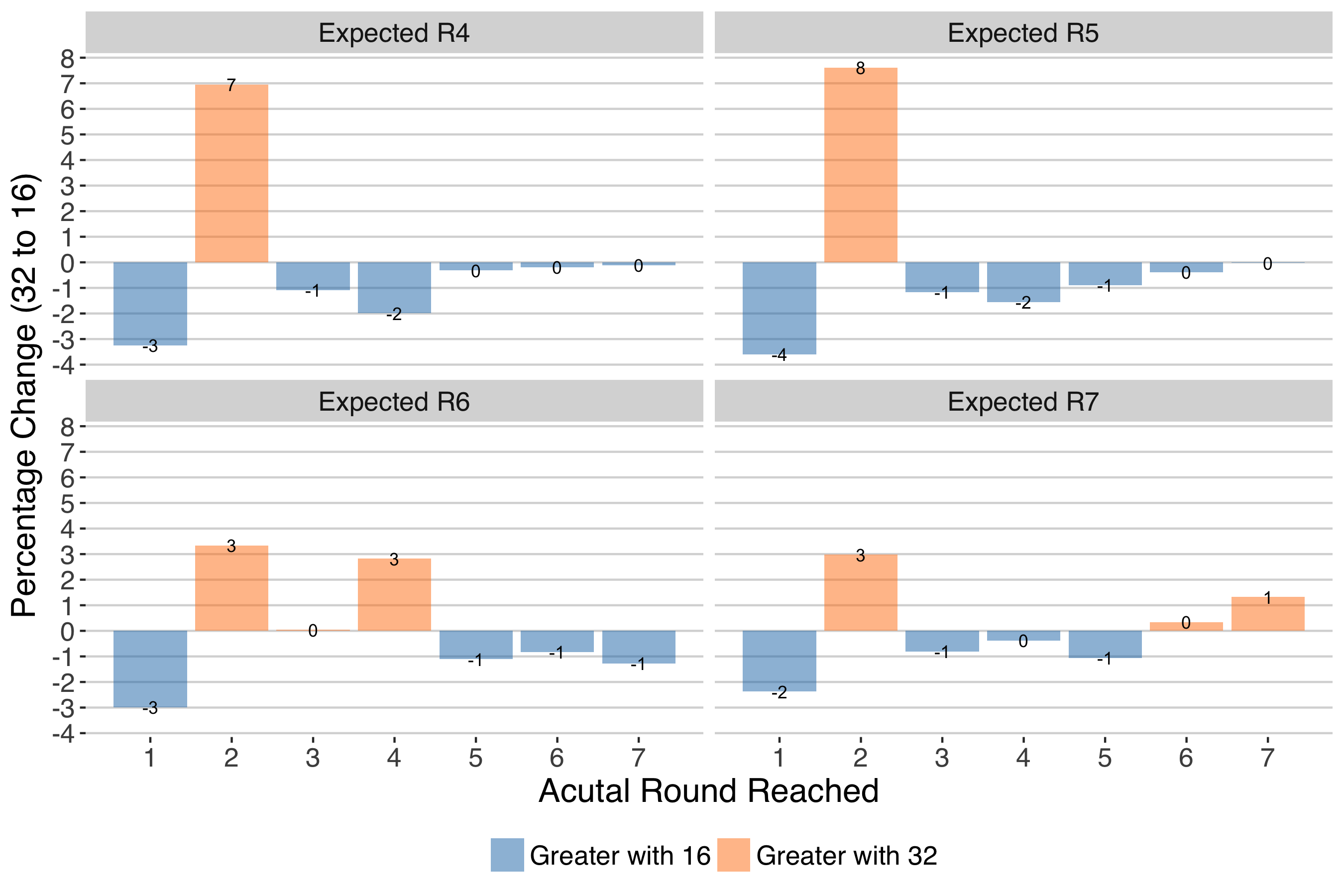
Actual and Expected Round Changes for R4-R7 with Men's 16-seed Grand Slam
The patterns in the actual and expected rounds reached were quite similar for the women’s draw for the first 3 rounds. However, rounds 4 thru the final showed some interesting differences. While the impact of the 32 seed largely centred around the first two rounds, we see that for the best players among the women, a 32-seed draw would have a much more pervasive trend in helping the stronger players to the later rounds.
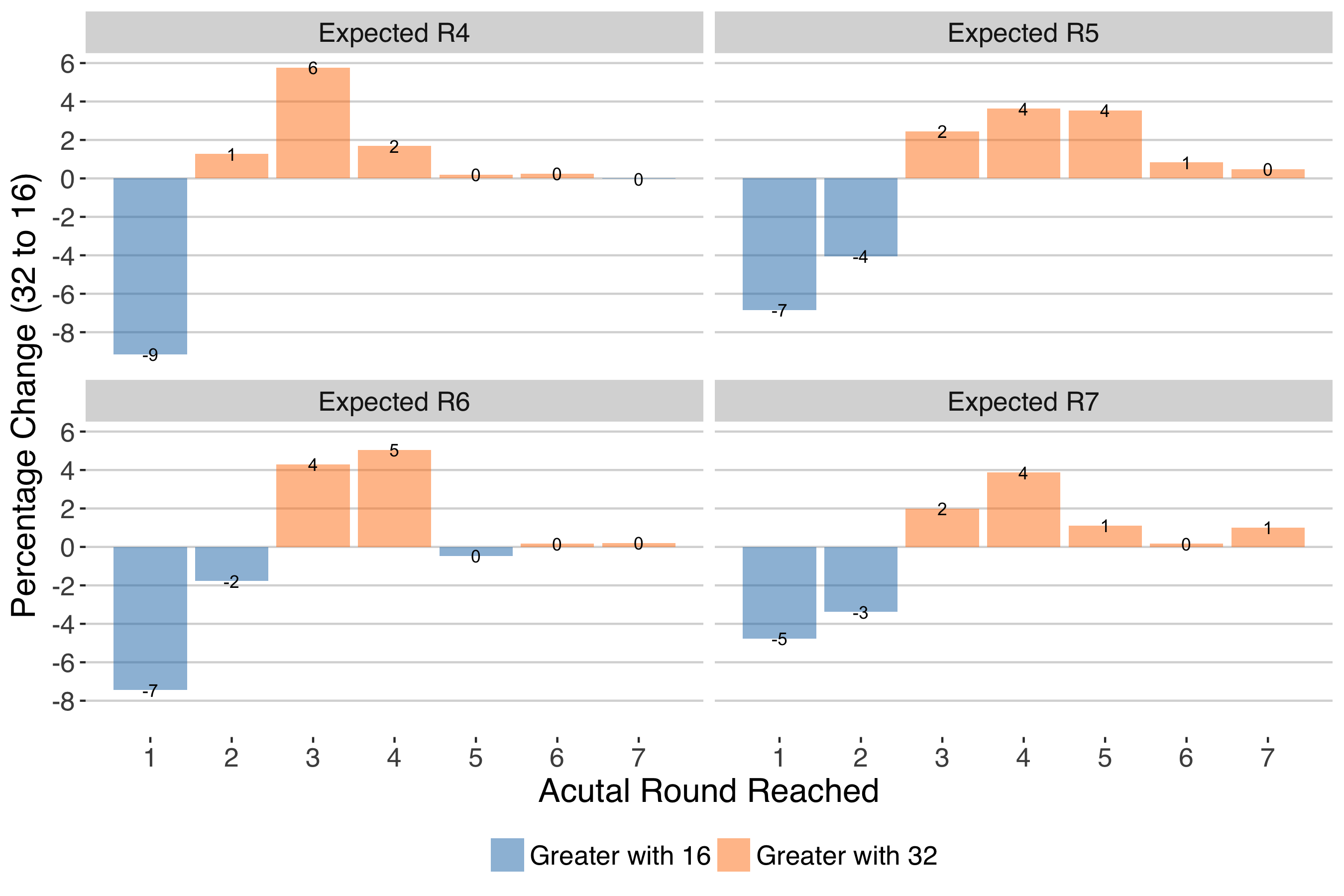
Actual and Expected Round Changes for R4-R7 with Women's 16-seed Grand Slam
Summary
This assessment of the possible impact of a change back to 16-seed Grand Slams suggests that there are grounds for player fears about early losses. For both men and women, the 2019 change can be expected to do a poorer job in picking the right winners in each round, reducing the chances that a player will reach their expected round by 5% overall. While there might be an argument that 16-seeds will bring more excitement to events, the expected frequency of close matches suggests that this will only be the case for the first few rounds, while rounds in the second week are expected to suffer by more frequent lopsided matches. This is especially the case for the women’s draw, which may have to do with differences in the depth of the tours in recent years.
Tennis shouldn’t be afraid to evolve but it is also important to ensure that adopted changes have a high potential to improve the sport and won’t simply be a change for change itself.

